Expressing the entire equation in terms of f1:
(f0)2=(yf1) * f1
Step4: Rearranging the above equation to express f1 in terms of f0
(f1)2=(f0)2/y
Therefore: f1 = √((f0)2/y)
If you use the negative sign then you will use the reverse: f1 = yf2 to solve for f2. And now you have solved f1 and f2 given the center frequency and Q.
Applications- Prevent Overlapping of Frequency Range during Boosting in Mixing
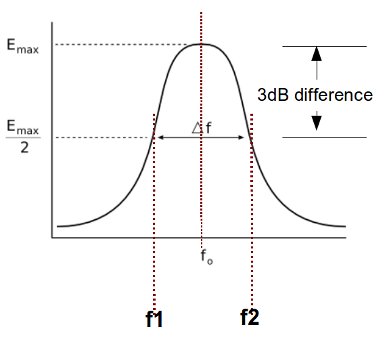
It would be exciting to apply what you have just learned in the previous section. In the above equations, it is possible to compute f1 and f2 provided you know the center frequency (f0) and Q:
In audio mixing, you will be using a parametric equalizer to shape the sound of your mix. One important considerations is to prevent overlapping adjustments in your EQ settings. For example, say you are mixing bass and kick drum. And you want the bass guitar to occupy the lower levels in the bass frequency spectrum while the kick drum would occupy the upper bass region. Then you decide to apply the following EQ settings:
Bass Guitar
Boost 50Hz, +3dB Q=1.0
Kick drum:
Boost 100Hz, +3dB Q=1.0
Question: Does the boost settings overlapped? Overlapping is undesirable as it will artificially boost certain frequency range that you are not intending to boost. You can analyze whether the EQ adjustments are overlapping by implementing the theory illustrated previously.
Let’s compute the f1 and f2 of the bass guitar parametric EQ adjustments:
Let’s compute Y first:
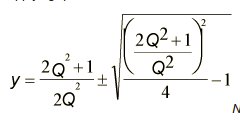
y= 0.38
y= 2.62
There are two values but the bigger value (2.62) is the result of the + sign. Let’s use that.
The compute f1 given the center frequency f0 and Y:
f1 = √((f0)2/y)
Solving f1 (use your calculator): 30.9Hz
Then f2 is equal to:
f2 = yf1
f2= (2.62)*(30.9)= 80.9Hz
Now for the kick drum EQ adjustment, solving for Y:
Y= 0.38
Y=2.62
It is the same because the Q is still set to 1.0 for the kick drum. Let’s still use the bigger value that is 2.62. Computing for f1:
f1= 61.78Hz
Now, its obvious that the boost settings overlapped because the lower value of kick drum adjustment that is 61.78Hz is within the f1 and f2 boundary of bass guitar adjustments (30.9Hz to 80.9Hz).
What is the solution in case of overlapping? You might to assign a tighter Q such as 2.0 instead of 1. If you use Q=2.0, then y=1.645 (using the bigger value). Then following are the f1 and f2 of the bass guitar and kick drums:
Bass guitar: f1=39Hz, f2=64Hz
Kick drums: f1=78Hz, f2=128Hz
See? There is no more overlapping since the bass f1 frequency level (78Hz) is now beyond bass guitar f2 (64Hz). Of course, you don’t need to this calculation everytime you are mixing. It is because modern parametric equalizers offer visuals, plots and graphs in addition to the settings so that you can directly observe if overlapping occurs.
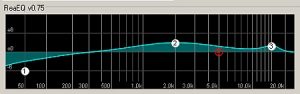
Without overlapping, you can be certain that there are no artificial boost on unintended frequency range. This is commonly caused by wide Q adjustment on your parametric equalizer.
Content last updated on August 22, 2012







No responses yet