First, if you do not have any idea of what 64-bit float means, then you need some introduction. When you are recording/tracking digitally, you are converting analog audio to digital audio data which are processed and stored in your computer.
Then if you are using a 24-bit audio interface (which is a standard in professional music productions), it will convert these analog data into 24-bit data (binary data in the series of 1 and 0) streams which are communicated via your Firewire or USB cable (depending on whether you are using a Firewire or USB audio interface).
64-bit float and 32-bit float
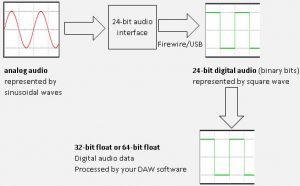
The actual resolution of your audio when saved into your hard disk drive is actually using 24-bits. However when processed by your DAW, it can either process the 24-bit audio data as:
a.) 32-bit float
b.) 64-bit float
Even though your DAW processes audio at any of these floating point systems, the source audio is still 24-bit and nothing is changed. The reason why they are processing it as a floating point is for convenience in the computation and representation of very large /very small numbers and efficiency. This makes it possible to retain resolution while doing complex computation thus benefiting audio quality during the mix. After all, your DAW would perform a lot of arithmetic calculations during the mixing process that includes:
a.) Implementation of plug-in effect settings.
b.) Setting levels.
c.) Digital summing of the mix (mix down or rendering the project)
The format of 64-bit float is similar to 32-bit float except that it accepts a wider range of bits. This is the 32-bit float format:
32 bit floating structure
Errors occurring during Digital Calculations in the Audio Mix
When you are mixing using a 32-bit float DAW, you would be applying effects or any digital manipulations to the audio. One downside of doing these digital calculations is not they cannot exactly represent all resulting numbers in the computation.
If you are confused why they cannot represent all resulting numbers, let’s start with decimal number system in which you are very familiar. Let say you are performing arithmetic calculations like dividing a number; if you divide 1 to 4 that is equal to 0.25. So it’s represented exactly. Another example is that if you divide 4 to 5, this is equal to 0.8. Again the result is an exact representation of the number.
However, if you divide 1/3 the result is 0.33333…. repeating infinitely. Thus you would need to round off say the first 3 digits of the result which is 0.333. This rounding off results it is not an exact representation of the actual results and this would introduce some errors.
The same if you divide 1/9 or 1/27 and there are many numbers. Going back to floating point arithmetic in binary, same concept applies. It cannot represent numbers such as 0.1 because of the same explanation/limitations as in decimal system. Converting the decimal 0.1 to binary will result to:
0.00011001100110011001100110011001…