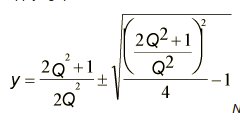This a very useful theory in the application of parametric equalizer in audio recording, mixing and mastering. The bandwidth (Δf) is given by a relationship:
Bandwidth =Center Frequency / Q
Definition of Bandwidth
In addition, the bandwidth is also defined as:
Bandwidth = f2 – f1
Where f1 and f2 are -3dB points in the peak amplitude for the center frequency (f0). Supposing a frequency boost using a parametric equalizer can be graphically depicted:
-3dB points (also known as “half power point”) means that the energy or loudness level drops by half. Supposing you will boost the center frequency by 12dB. The -3dB point (point at which the loudness level drops by half) is 12/2= 6dB.
When you cut a frequency level, say for example cutting -8dB on a certain frequency band, the -3dB point is -8dB/2 or -4dB.
In audio mixing, two values are needed to define as EQ setting (like what most EQ suggestions you find in audio recording website). One is the center frequency and the other is the Q. This is because most parametric equalizers need that setting (EQ and Q) to define a frequency adjustment. You might notice that parametric equalizers in Adobe Audition or other DAW do have the same requirements.
The Q is also a measure of how wide or narrow is the frequency adjustment. Large Q means wide frequency adjustment and small Q means small frequency adjustment.
Computing f given Q and the center frequency
It would be interesting to compute f1 and f2 provided that you know the Q and the center frequency.
Given:
f2 = yf1 where y could be any positive real number
And also f0 = √(f2 * f1)
Source: http://www.rane.com/note170.html
Using all the above equations, the y can be derived in terms of Q:
Take note that y can have two values due to the ±. if you use the – sign, then:
f1 = yf2
And if you use the + sign then:
f2 = yf1
The important is to remember that f2 > f1
Approach to solving f1 and f2, given Q and the center frequency:
Step1. Solve y from the above equation by substituting the given value of Q.
Step2. Once the y is solved (two possible y values), substitute y value to
f2 = yf1 for the use of + sign or f1 = yf2 for the use of – sign.
Step3: Now since f0 = √(f2 * f1), then squaring both sides:
(f0)2=f2 * f1
Now supposing you use the + sign in the calculation of y then:
f2 = yf1